最近在学习深度学习机器学习的相关内容，神经网络算法确实是有很多应用的场景，也非常值得学习和探讨，因此在学习中记录下来，也大家交流。
题外话
这里抛出一个问题，人是如何从出生到慢慢长大的过程中记忆生活中的一些东西的？生物在外界刺激的条件下是如何建立反馈机制的？相信学过生物的同学肯定听说过神经元也就是神经细胞，它的定义是神经系统中负责神经传导的基本结构和功能单位。下图是一个典型的神经元结构：
(摘自：https://zh.wikipedia.org/wiki/%E7%A5%9E%E7%B6%93%E5%85%83#/media/File:Complete_neuron_cell_diagram_zh.svg)
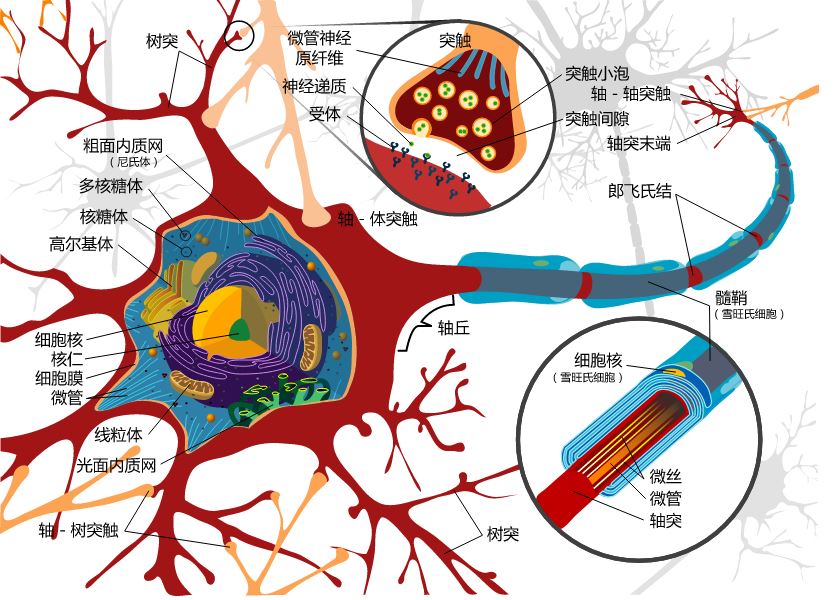
其实在生物体的神经结构中，有很多神经元，这些神经元间相互联系形成了网状结构，构成了生物学中的神经网络。人脑大约由140亿个神经元组成，而其中的每个神经元又与约100～10000个其他神经元相连接，构成了一个非常庞大而复杂的神经元网络。
那么他们间是如何传递信息的呢？当神经元接收到信号刺激时，就会引起神经元兴奋或者抑制，并通过轴突向突触释放电信号或者化学信号产生神经元间信号的传递。当然，这些突触并非对于所有的刺激都是敏感的，所以产生了对于不同信号传播的途径不同的情况，例如人的皮肤不能感受光线的刺激。从而不同的刺激被传递到不同的大脑区域进行处理分析。
经过科学家长期对于神经网络的机理的研究，也确实得到了一些成就，但远远达不到解释人类精神活动，意识形态的层面。但他们从神经细胞结构及神经网络组成的水平上初步探明了大脑的组织特征，这也使得我们在计算机领域针对人的大脑活动有了参考的模型。就是这里要阐述的人工神经网络。人工神经网络就是在基于生物神经网络特征，建立的神经元和神经网络的数学模型。这里的模型相对于真实的神经网络来说，是一个足够简化的版本，是对神经网络的抽象和模拟。
神经网络算法简介
在机器学习和认知科学领域，人工神经网络（artificial neural network，缩写ANN），简称神经网络（neural network，缩写NN）或类神经网络，是一种模仿生物神经网络(动物的中枢神经系统，特别是大脑)的结构和功能的数学模型或计算模型，用于对函数进行估计或近似处理。
神经网络的出现也正是模仿生物神经网络的反馈机制建立的数学模型。最著名的神经网络算法是1980年提出的”反向传播算法”（backpropagation），简称BP。
在理解人工神经网络算法之前，需要了解一个概念：人工神经元模型。
人工神经元模型（Neuron Modle）
一个人工神经元的抽象数学模型如下所示：
我们联想生物神经元的信息处理能够发现，一个神经元有若干个树突，这些树突和其他神经元的轴突神经末梢连接。信号传递的方向是从轴突神经末梢的突触传递到下一个神经元的树突。类似的，一个人工神经元模型由若干个输入和一个输出组成。中间进行了一系列的数学运算。每一个输入都有一个权重w，我们可以理解为轴突给树突的信号强度。这样，不同的刺激其他神经元传过来，被树突接收，我们如何处理这些刺激呢？当然是优先响应信号轻度大的。在人工神经元模型中我们需要对这些输入值乘以权重然后加权求和，在加上偏向量作为f函数的输入。f函数指的是激活方程或者响应函数（Activation Function）,用于将数据进行非线性转化，通常使用sigmoid 转换方程。
激活方程的主要作用主要有以下三点： 1 控制输入对输出的激活作用； 2 对输入、输出进行函数转换； 3 将可能无限域的输入变换成指定的有限范围内的输出。
对于多层的神经网络，常使用log-sigmoid、 tan-sigmoid方程，这个方程将输入转化为一个0-1之间的值，其公式如下：
log-sigmoid
tan-sigmoid
在一些特殊情况下，也可能是用线性方程作为激活方程。
经过以上步骤后，神经元就算是处理了来自多个输入端的数据，并将数据结果输出到下一个神经元。
多层向前神经网络
有了神经元模型的概念之后，就对于神经网络的建立没有那么多神秘感了。这里着重介绍下神经网络算法中的最早被提出也是最简单的神经网络模型 —— 多层向前神经网络（Multiplayer Feed-Forward Neural Network）.
多层向前神经网络也称为有理式多层前馈神经网络，由一个输入层，一个输出层和若干个隐藏层组成，在它内部，参数从输入层向输出层单向传播。其结构如下图：
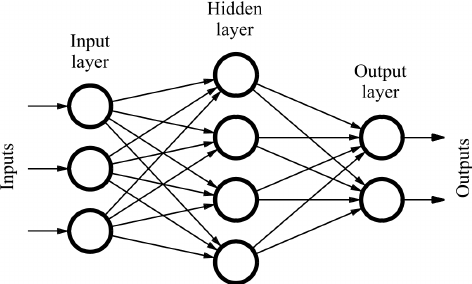
对于这种神经网络，有以下特点：
- 每个层由若干个基本单元组成
- 数据集通过输入层传入到神经网络中进行计算，这些数据是特征集的特征实例变量。
- 经过输入层再由连接节点的权重经过一系列的计算传入到下一层，直到传输到输出层为止
- 中间的隐藏层可以有N多个
- 每个单元被称为神经节点
- 通常在计算神经网络的层数时，输入层不计算在内
- 在计算输出的过程中，对每一层的单元进行加权求和，在进行非线性的方程转化后作为结果输出到下一层
- 理论上讲，在隐藏层足够多，训练集足够大的情况下，我们是可以拟合任何方程的。
多层向前神经网络的设计
在设计神经网络的过程中通常需要考虑一下两个问题：
- 隐藏层该设计多少层
- 每层有多少个单元
为了使得出入值能够更加快速有效的被计算，加快算法的学习过程，通常情况下还需要对输入层进行标准化（normalize），这个过程会将输入通过方程转化为0-1之间的值。 输入集合有可能是连续的值，例如1-100之间的任意值，也可能是离散的值，例如1-100之间的整数，那么这些值如何表示到输入层上也就成了问题。
神经网络既能够支持连续值也能够支持离散值，对于离散型的变量，我们通常将其所有可能值的每个值作为一个输入单元的数据进行编码，可以理解为一个输入单元和其他单元互斥，当代表某个值的单元表示为1，则其他单元表示为0，此时，这个输入的离散值就是表示为1的单元对应的值。
神经网络既可以解决回归问题，也能够解决分类问题。对于分类问题，如果分类结果只有两种类型，只需要一个输入单元即可表示。如果有多个类，我们对于每一个类用一个输出单元表示即可。因此，输出层的数量通常是类别的数量。
对于隐藏层的设计，没有具体的定义设置多少层，因此需要通过实验和训练结果进行测试设定。
算法实现 —— backpropagation 算法
反向传播算法通过迭代性来处理训练集中的实例，通过对比经过神经网络后的输入层预测值和真实值之间的误差，反方向从输出层到隐藏层再到输入层更新每个节点的权重和偏向来最小化误差。
参考文献
- https://zh.wikipedia.org/wiki/%E4%BA%BA%E5%B7%A5%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C
- http://www.fon.hum.uva.nl/praat/manual/Feedforward_neural_networks_1__What_is_a_feedforward_ne.html
- http://www.eis.mdx.ac.uk/staffpages/rvb/teaching/BIS3226/hand11.pdf
- https://en.wikipedia.org/wiki/Feedforward_neural_network
- https://www.med.nyu.edu/chibi/sites/default/files/chibi/file2.pdf
- https://cn.mathworks.com/help/nnet/ref/feedforwardnet.html?requestedDomain=www.mathworks.com
- https://cn.mathworks.com/help/nnet/ug/multilayer-neural-network-architecture.html
- http://www-rohan.sdsu.edu/doc/matlab/toolbox/nnet/backpr52.html
- http://www.cs.cmu.edu/~rsalakhu/papers/sfnn.pdf
- http://www.bb.ustc.edu.cn/jpkc/xiaoji/jswl/ch9.pdf
- http://blog.163.com/zzz216@yeah/blog/static/16255468420107863920341/
